Pharmacokinetics
What the body does to the drug.
Bioavailability
$F = \frac{\text{quantity in circulation}}{\text{quantity administered}}$
The most common method of absorption is via passive diffusion, which means the drug must be non-polar enough to cross membranes, but polar enough to dissolve in water.
$\frac{\text{unprotonated}}{\text{protonated}} = 10^{pH - pKa}$
$log(\frac{\text{unprotonated}}{\text{protonated}}) = pH - pKa$
Depending on the pH of the target body compartment, the drug's pKa will determine if the drug is polar or non-polar. Acids should be at a low pH to be absorbed, while bases should be at a high pH to be absorbed.
1. Liberation
Process of releasing the drug from its packaging. An extended release capsule, for example.
Delayed release (DR)
The Tmax (time to maximum plasma concentration) is longer than the immediate release (IR) form.
Continuous release
Has a staggered release schedule in the body which creates a stable plasma concentration over a longer period of time. An example is enteric coating, which is stable at acidic pH but breaks down at a basic pH in the small intestine. This frees up more of the drug for absorption further down the GI tract.
2. Absorption
Oral & Rectal
Absorbed through the GI tract, subject to first-pass in the liver. Safe and convenient. Delivery to the distal 1/3 rectum allows for greater bioavailability by avoiding some of the first-pass. Not all patients are on board with boofing.
Bioavailability: 5% (0.05)
Bioavailability (with rectal bypass): 30% (0.3)
Subcutaneous/Percutaneous
Absorbed through/under the skin. Does not work with large volumes.
Bioavailability: 75% (0.75)
Intravenous
Administered to the plasma. Fasted method of delivery.
Bioavailability: 100% (1.0)
Intramuscular
Absorbed through the muscle via injection. Does not work with large volumes.
Bioavailability: 75% (0.75)
Intrathecal
Administered through CSF, which is great for drugs targeting the brain.
Bioavailability: 100% (1.0)
Inhalation
Absorbed through the lungs and deposited into blood. Good for lung targets. Can be exhaled before absorption.
Bioavailability: Varies by particle size
Bonus: Intraosseous
Administered into the medullary bone with a drill and enters circulation with venous channels. Good for combat medicine as the linkage is very stable. It's also interesting as it doesn't hurt going in, but pushing fluid is astonishingly painful. Pros: Metal as fuck.
Bioavailability: 100% (1)
Check this out: https://www.youtube.com/watch?v=MgQJIsavbjI
3. Distribution
Plasma proteins
Plasma proteins can non-specifically bind to drugs to keep them from acting on target tissues. These impact how long a drug stays in the body and the concentration available to receptors.
Albumin: Binds acidic or neutral drugs
Alpha-1-acid glycoprotein (AAG): Binds basic drugs
P-glycoprotein (P-gp): Transports drugs in and out of tissues, especially in the blood brain barrier.
Clinical peal: Warfarin
Warfarin has a narrow therapeutic index and is highly bound by plasma proteins. When another drug competes with plasma protein binding, it will displace the warfarin and increase bleeding risk.
Drug diffusion
Recall: The average individual is 70kg (42L TBW) with 4L plasma, 10L interstitial fluid, and 28L intracellular fluid.
If a drug is small enough, it can pass from plasma to interstitial fluid.
If a drug has the correct pKa, it can pass into the cell.
A drug both small enough and with the correct pKa will have access to all fluid compartments and is considered flow limited. The distribution of these drugs is limited only by the level of blood flow to a given tissue. This will effect timing of therapeutic action.
Drugs which cannot pass through membranes are considered membrane limited.
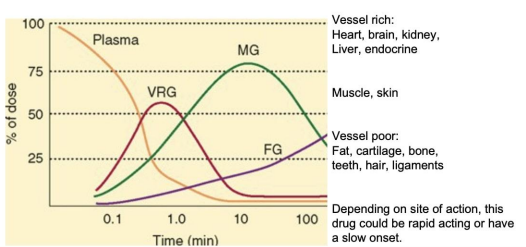
Multiple compartment model
- Alpha phase (distribution): Rapid decline in plasma concentration as the drug enters tissues
- Beta phase (elimination): Drug has reached equilibrium and the decline in plasma concentration comes from excretion (elimination)
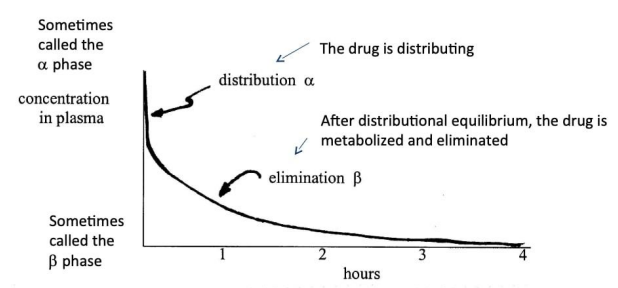
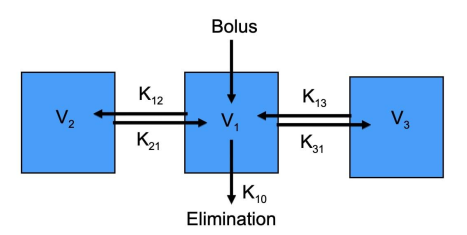
Two compartment example
An IV bolus entering into the central compartment. The rate into V2 is determined by K1→2 and K2→1. Elimination is represented by K1→0.
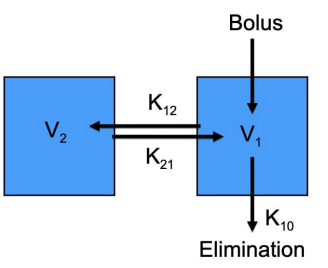
Three compartment example
Similar to the two compartments, with additional vectors K1→3 and K3→1. Complexity increases arbitrarily with the number of compartments and their interactions.
4. Metabolism
See here: Drug Metabolism
5. Elimination
The majority of drugs are excreted via the kidneys (urine). 80% of drugs are transported into the proximal tubule for excretion. 20% of drugs are non-polar and passively diffuse from blood to urine. However, these can follow the concentration gradients and diffuse back.
To excrete non-polar drugs, the pH of the urine in the distal tubule is altered to change the polarity of the molecule in a process called ion trapping.
Clearance rate
Most drugs are first order, with the amount eliminated being proportional to the concentration in the bloodstream. When drug concentration is higher, so is metabolism. Metabolic (ladMe) enzymes are more abundant than drug concentration and will not be saturated, generally sitting below Km.
A constant fraction of the drug is eliminated per unit time. The time it takes to eliminate 50% of the drug is referred to as half-life. Four-half lives will clear 90% of the drug and can be expressed as follows:
$90% < 4 \times t_{\frac{1}{2}}$
t1/2 = half-life
The decay in the concentration of the drug is exponential.
$C = e^{-k_et}(C_0)$
C = concentration at time t
e = 2.7 (constant)
Ke = rate constant of elimination
C0 = initial concentration
$t_{\frac{1}{2}}$ can be also be defined as $t_{\frac{1}{2}} = \frac{0.69}{K_e}$. For example, if Ke = 0.1 units/hr, 10% of the drug will be eliminated in an hour.
The decay can also be expressed in linear form, where slope is -Kc/Kb, and the Y-intercept is the natural log (ln) of the starting concentration.
$ln(C) = -kt + ln(C_0)$
Enzyme saturation
When drugs do saturate the enzymes, there are a constant number of molecules being eliminated over time. Thus, these reactions are zero order and do not use a concept of half life.
Examples of zero order drugs: Ethanol, phenytoin, fluoxetine, verapamil.
Volume of distribution
The apparent volume in which the drug is dissolved. Analogous to V = Q/C.
$V_d = \frac{D}{C_o}$
D = dosage (drug quantity)
C0 = initial concentration
To find the dosage to achieve a target concentration, the following can be used to calculate loading dose.
$D = C_0 \times V_d$
Vd = compartment volume
C0 = initial concentration
Note: In some cases the volume of distribution can be larger than the person (e.g. 100L > 42L). In these cases, the drug will have dissolved into the fat tissue.
Steady State
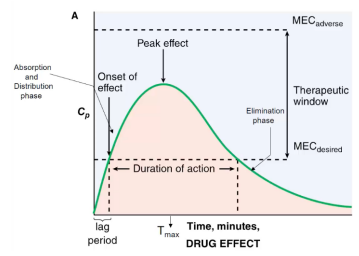
The area under the curve (AUC) is the amount of drug the body metabolizes. In the following figure, the minimum effective concentration desired (MECd) signifies the concentration when an effect will occur. The peak effect occurs at concentration Cmax and time Tmax.
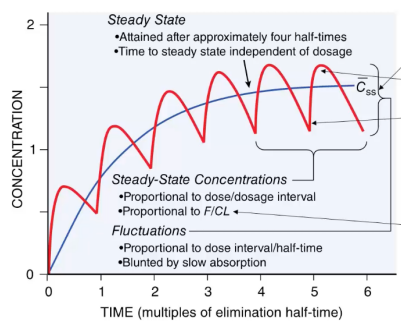
Many drugs are administered in multiple doses with a steady state target, when the intake and elimination are at equilibrium. You'll see some cyclical variation in the plasma concentration before reaching steady state. This only occurs with routes with bioavailability (F) < 1 because the decreased bioavailability might mean the drug has to be titrated to avoid toxic effects of trying to hit the steady state with a high starter dose.
Clearance
Allows calculation of dosing rate to maintain a steady-state. Is is found using the volume of distribution (Vd) and the fraction of Vd being eliminated (Ke).
$CR = K_e \times V_d$
Therefore, the dosing rate (the amount of drug going in) will equal the amount of drug going out (clearance * concentration at steady state). This can be expressed as follows:
$DR = CR \times C_{SS}$
CR = clearance rate
Css = concentration at steady state
Cases where F < 1
For routes where the bioavailability isn't 100%, the equation should be modified to increase the dosing rate (remember 0 < F < 1).
$DR = \frac{CR \times C_{SS}}{F}$
CR = clearance rate
Css = concentration at steady state
F = bioavailability
The same is true for finding the steady state concentration, which will be reduced with fraction of F.
$C_{SS} = \frac{F \times \text{dose}}{CR \times \text{time}}$
F = bioavailability
dose (mg) = quantity administered
CR (mg/time) = clearance rate
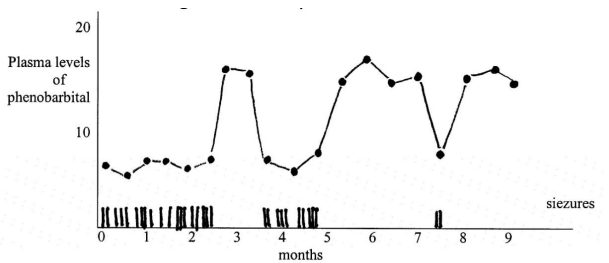
Clinical pearl: Phenobarbital
Phenobarbital is an anti-seizure medication. When plasma levels fall out of therapeutic range, more seizures are observed. This allows clinicians to determine dosage.
