Resting Potential

Fluid Mosaic Model

Components of the cell membrane move around as determined by concentrations of cholesterol, saturated/unsaturated fatty acids, and temperature.

Fick's Law

Flux is a measurement of particles moving down a concentration gradient per unit time.

$J_i = D_i A \frac{C_1 - C_2}{x}$

J = flux
Di = diffusion coefficient
A = cross sectional area
(C1 - C2) = concentration difference
X = distance over which the diffusion takes place

Flux is driven by concentration difference (C1 - C2) as the other parameters are fixed.

Movement through membranes

Fick's law will apply to cells membranes as well.

$J_x = P_x (X_o - X_i)$

Jx = flux
Px = permeability coefficient
(Xo - Xi) = concentration difference between outside (o) and inside (i) the cell

Px is determined by four components

• Lipid/water coefficient: Ratio of a molecule's solubility in oil vs. water. 1 is fully lipophilic, 0 is fully hydrophilic.
• Diffusion coefficient
• Membrane thickness
• Membrane area

Ion Channels

Ions can freely diffuse in and out of pores (e.g. non-gated channel or leak channel). The number/type of pore channels determines the resting membrane potential (RMP).

Gated channels, by contrast, open and close in response to a stimulus (e.g., light, sound, voltage, etc.). They can also alter the flux of an ion.

Voltage-Gated Channels

Components:

• Gate
• Ion selectivity filter
• Voltage sensor (can be ligand binding)
• Glycoproteins
• Anchor proteins

Structure

Subunits consist of 6 transmembrane helices. Hydrophilic amino acids will be on the outside and can be plotted using the amino acid residues. This reveals which portion of the membrane is in the cell.

NOTE: The pore domain is not counted as a transmembrane helix. This is why there are 7 spikes instead of the expected 6.

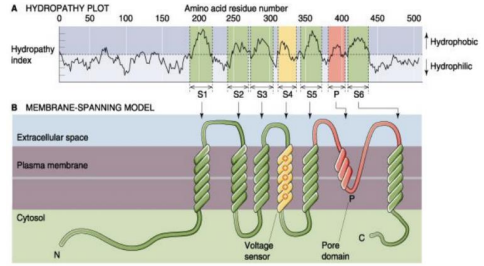
Channels can also be made up of different numbers of subunits.

• Tetramer (4): Na+/K+/Ca2+ channels
• Pentamer (5): Nicotinic Acetylcholine
• Hexamer (6): Connexon, making up half of a gap junction channel.

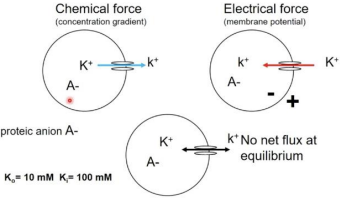
Electrochemical Equilibrium

Chemical force: Concentration gradient
Electrical force: Charge buildup (electrical gradient)

Nernst equation

Measuring the equilibrium potential for an ion

$E_{eq} = \frac{2.3RT}{zF} * log(\frac{[X_o]}{[X_i]})$

RT = gas constant * absolute temperature
z = valence (charge of ion, Ca2+ = 2, K+ = 1)
F = faraday's constant

Simplified: $E_{eq} = \frac{60}{z} * log(\frac{[X_o]}{[X_i]})$

memorize this pls

Depolarization and Hyperpolarization

Depolarization occurs as the membrane becomes less negative. Hyperpolarization occurs as the cells becomes more negative then its resting state.

Resting membrane potential

As ions flow over the cell membrane, they produce current. At steady state, the currents from sodium and potassium cancel each other out. Therefore, $I_K + I_{Na} = 0$.

The sodium-potassium pump will maintain the cell membrane potential as the leak channels freely move ions in and out of the cell. The leak channels will usually be permeable to one ion at a time, which creates the gradient.

Membrane Conductance

The membrane potential is the differences in voltages inside and outside the cell.

Voltage

Ohms law states V = IR

V = voltage
I = current
R = resistance

Conductance (G) is the opposite of the resistance (1/R). Therefore, V = I/G.

Capacitance

Capacitance is the ability of a system to store charge. C = q/V

C = capacitance
q = charge (coulombs)
V = voltage

Multi-Ion Membrane Potential

Modification of Nernst into Goldman-Hodgkin-Katz. This example considers Na2+ and K+.
$$V_m = -60 * log(\frac{G_{\text{Na}} * [Na]{\text{out}} + G{\text{K}} * [K]{\text{out}}}{G{\text{Na}} * [Na]{\text{in}} + G{\text{K}} *[K]{\text{in}}})$$
Current equation:
$I = G(V_m - E{eq})$

I = current
G = conductance
(Vm - Eeq) = driving force

At steady state for the ions Na2+ and K+, the following would be the derived equation:
$I_{Na} + I_K = 0$

Therefore:
$I_{Na} = G_{Na}(V_m - E_{Na})$
$I_{K} = G_{K}(V_m - E_{K})$

And finally to combine into the Goldman-Hodgkin-Katz (in steady state):

$V_m = \frac{(E_{Na} * G_{Na}) + (E_K * G_K)}{G_{Na} + G_K}$

Key takeaways

Driving force (Vm - Eeq) determines ion flux and direction.

For cations, positive current represents outward flow.
For anions, positive current represents inward flow.